TEMEL FİZİK YASALARI

Hepimizin sürekli duyduğu, okullarda görmemize rağmen bazen unuttuğumuz bazen karıştırdığımız bazı temel yasaları sizler için bir araya getirerek en basit şekilde bahsettim.

Newton’un Üç Temel Hareket Yasası

Isaac Newton kuvvet ve hareket arasındaki ilişkiyi  3 temel yasa ile açıklamıştır.

1)Eylemsizlik:

Eylemsizlik, kelime anlamı olarak bir cisme, bir dış etki bulunmadığı sürece, hareket durumunun değişmeme özelliğidir. Newton eylemsizlik yasasını da şöyle açıklar,  Sabit kabul edilen bir referans noktasına göre eğer cisme etki eden bileşke kuvvet sıfır ise(Fnet=0), cisim duruyorsa durmasına devam eder(v=0), hareketli ise  sabit hızla hareketine devam eder(v=sbt). Yani cisim durumunu korur. eylemsizliği bu durumda  bir cismin süratinin veya  yönünün değişmesine karşı koyması da diyebiliriz.

Buna basit bir örnek ise duran bir arabanın aniden hareket etmesi ile içindeki yolcuların geriye doğru gitmelerinin sebebi eylemsizliktir. Yani eski hareketsiz konumunu koruma isteğinden dolayı yolcular direnç gösteriyor.

2)Dinamiğin Temel Prensibi (İvme):

Bir cisme etki eden kuvvetlerin bileşkesi sıfır değilse (Fnet≠0), cisim ivme kazanır. Net kuvvet cimin hareketi yönünde ise cisim hızlanır, zıt yönde ise önce yavaşlar durur daha sonra zıt yönde hız kazanır. Net kuvvet vektörüyle ivme vektörünün yönü her zaman aynıdır. Kuvvetin, cisme kazandırdığı ivmeye oranı sabit olup, bu sabit değer ise cismin kütlesine eşittir  ve aşağıdaki formülle ifade edilir.

F=m.a

m: kütle (kg)

F(Fnet): cisme uygulanan net kuvvet (N)

a: ivme (m/s²⁾

3)Etki-Tepki:

Bir cisme kuvvet uygulandığında cisim de kuvvet kaynağına aynı büyüklükte ve zıt yönde kuvvet uygular. Etki tepki kuvvetleri birbirine eşittir fakat cisimler farklı olduğu için birbirlerini dengeleyemez.  Yani aynı cisimler üzerine kuvvet uygulanmaz dolayısıyla bileşkesi alınamaz ve sıfır değildir.

Örneğin; bir topu duvara attığımızda duvara çarpması ile duvar da aynı kuvveti topa uygulayarak geri itmesini sağlar.

 

Enerjinin Korunumu Yasası

Enerjinin korunumu yasası enerjinin yoktan var olmayacağını ve vardan yok olmayacağını ancak başka bir enerji türüne dönüşebileceğini açıklar. Enerji dönüşürken de kayıp olmaz yani o sistemde toplam enerji miktarının sabit kalacağını söyler. Örneğin potansiyel enerji kinetik enerjiye dönüşebilir ya da kinetik enerji potansiyel enerjiye dönüşebilir.

Dediğimiz gibi enerjinin korunum yasası yalıtılmış, kapalı sistemler için geçerlidir. Mesela bir zemin üzerinde yuvarlanan bir top, enerji korunumu kanununa uymaz. Çünkü zeminle temas ederken enerjinin bir kısmını ona devredecektir.

Mekanik Enerjinin Korunması

Mekanik enerji bir sistemdeki potansiyel enerjinin ve kinetik enerjinin toplamıdır.

E_M = E_P + E_K

 

Momentumun Korunumu Yasası

Momentumun korunum yasası aslında Newton’un 3. hareket yasasına bağlı olarak doğuyor. Yani cisme etkiyen kuvvet, her zaman kendisine eşit ve zıt yönde bir tepki kuvveti doğurduğundan sisteme etkiyen kuvvetler birbirini dengelemektedir. Momentum, kuvvetin zamana göre türeviyle elde edileceğinden ve zamandan bağımsız olarak kuvvetler dengelendiğinden dolayı sisteme ek momentum girdisi olmayacaktır. Yani sistemdeki maddelerin momentumları toplamı, incelenen zaman aralığı ne kadar uzun olursa olsun sıfır olacaktır. Eğer sistemin bir bölümüne bir yönde momentum kazandırılırsa, sistemin diğer bölümleri tam olarak aynı büyüklükte momentumu zıt yönde kazanır. Yani sistemin toplam momentumu korunur.

Momentumun korunumu sadece nesnelerden oluşan izole bir sistem için geçerlidir ve şu matematiksel ifadeyle gösterilir:

P = m.v

m: hareket halindeki cismin kütlesi (kg)

v: cismin hızı (m/s)

P: cismin momentumu (kg.m/s)

Bir sistemdeki tüm cisimlerin m.v momentumlarının vektörel toplamı da, sistemin toplam momentumunu verir.

Kütle-Enerji Eşitliği 

En çok bilinen E=mc² denklemi diyor ki; eğer kütle enerjiye dönüşürse, ışık hızının karesiyle kütle büyüklüğünün çarpımı miktarında enerji ortaya çıkar. Bu durumda denkleme göre madde enerjiye, enerji maddeye dönüşebilir diyebiliriz.  E:Enerji (j) , m: Kütle (kg), c: Işık hızını(m/s) temsil etmektedir ve ışık hızı sabit olduğu için, bu formül bize enerji ve kütlenin birbiriyle aynı şeyler olduğunu söylemektedir. Einstein, cismin enerji yaydıkça kütlesinin azaldığını ortaya koydu ve  bu mantıkla, cismin kütlesinin, içerdiği enerji miktarının bir ölçüsü olduğu sonucuna vardı. Böylelikle enerji ve kütle arasında bir denklem yarattı. Fakat Einstein’ın özel izafiyet teorisiyle ilişkili bu denklemi özel bir durumda geçerlidir. Analiz edilen sistem hareketsiz olması (herhangi bir hıza sahip olmaması) durumunda ve analiz edilen sistemin hem enerjisi, hem de kütlesinin göreli olduğu durumlarında geçerlidir. Bir diğer deyişle, eğer ki sistemin sıfırdan farklı bir toplam momentumu varsa,  E=m.c²  formülü geçersiz kalır.

 

Gauss Yasası

Bir yüzeyden geçen elektrik akısı bu yüzeyden geçen elektrik alan çizgi sayısı ile doğru orantılıdır. Elektrik alan çizgileri kapalı yüzeyden içeri giriyorsa negatif, çıkıyorsa pozitif elektrik akısı oluşturur ve yüzeyin içerisinde hiç bir şey olmadığını varsayarsak giren çizgilerin hepsi tekrar çıkacak ve akı sıfır olacaktır.

Eğer kapalı yüzey içerisinde yük varsa ve bu yük negatif bir yük ise, içeri giren çizginin bir kısmı bu yük üzerinde biteceği için daha az sayıda elektrik alan çizgisi çıkar ve akı negatif olur. Eğer içeride pozitif bir yük var ise, bu yük üzerinde elektrik alan çizgiler başlar ve içeri giren çizgi ile beraber yüzeyden çıkar. Yani pozitif bir akı olur. İşte bu bağlantıyı  Gauss Yasası ile açıklanır.

∫E.dA = Qiç/ε0

E: elektrik alanı

dA: kapalı yüzeyin diferansiyel alanı

Qiç: kapalı alanın içindeki yük

ε0: elektrik sabiti (8.85*10 ^–12 )

Faraday Yasası (İndüksiyon Kanunu)

Faraday, kapalı bir devre içinde bir mıknatıs gezdirmesi halinde, mıknatıs hareket ettiği sürece devrede akım olduğunu keşfetti.  Bu etkiye elektromanyetik indüksiyon denir. Yani indüksiyon yasasına göre manyetik alan içinde bulunan bir iletkenin oluşturduğu ve zamanla değişen akı, iletkenin uçlarında gerilim endüklenmesini sağlar.

N sarımlı bir bobin manyetik alan içine sokulduğunda iletken üzerinden akım akar ve ve tel üzerinde elektromotorkuvvet oluşur. Oluşan elektromotorkuvvet kendini oluşturan akıya zıt yöndedir.

Oluşan gerilim yani elektromotorkuvvet;   e=-N.dΦ/dt  ‘dir.

Akı (Φ) zamanla değiştiği için zamanın bir fonksiyonu olarak ifade edilebilir. Zaten dΦ/dt nin sıfır olmaması için Φ nin zamanın bir fonksiyonu olması gerektiği görülmektedir.

e: elektromotorkuvvet (V)

Φ: akı (Weber)

N: sarım sayısı

Lenz Kanunu

Lenz kanunu, Faraday yasasında bahsedilen indüksiyon akımının yönünü belirler. İndüksiyon akımının yönü manyetik akı değişimine karşı koyacak yönde oluştuğunu ifade eder yani kendini oluşturan sebebe karşı zıt yönde oluşur. Faraday yasası formülünde ki (e=- NdΦ/dt ) (-) işaretinin nedeni budur.

Manyetik akının oluşması için manyetik alanın olması gerekir dedik. Burada manyetik alan yoğunluğunu B(Tesla) ve bu manayetik alan içerisinde bulunan iletkenin süpürdüğü alanı ise A [m2] ile gösterirsek manyetik akı Φ=BA olur.

Bu manyetik alan içerisinde l uzunluğunda ki bir iletken v (m/s) hızı ile hareket ettirilirse yine o iletkenin uçlarında bir gerilim indüklenir.

E=B.v.l

Ayrıca bu sistem generatör hareketinin de temelini oluşturur. Aslında Faraday ve lenz kanunu, elektrik makinelerinde kullanılan ve elektrik makinelerinin çalışma prensiplerini açıklayan temel yasalardan ikisidir.

Ampere Yasası

Ampere yasası için; herhangi bir kapalı yol, halka üzerinde alınan ∮B ⋅dℓ  integrali, bu kapalı yolun sınırlandırdığı alandan geçen toplam akım ile μo değerinin çarpımına eşittir, ifadesini hep duyuyoruz. Peki bu ifade ne demek?

Amper yasasına göre içinden akım akan bir iletkenin etrafında manyetik alan oluşur. Oluşan manyetik alanın yönü akımın yönüne göre değişir ve iki şekilde bulunabilir. Bunlardan biri sağ el kuralı, diğeri ise sağ vida kuralıdır.

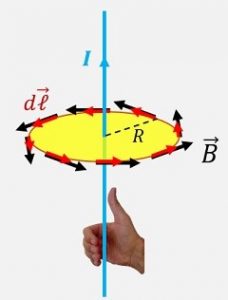
Sağ el kuralından (sağ elin baş parmağı akım yönünü, diğer parmaklar ise manyetik alanın yönünü gösterir) şekildeki gibi akım geçen bir telin etrafında manyetik alan (siyah oklar)  şekildeki gibidir. Manyetik alan halkaya her zaman teğet olacaktır. Halka üzerindeki bütün noktalar tele aynı uzaklıkta olduğu için manyetik alan halka üzerinde her yerde aynı büyüklüğe sahiptir. Halkanın küçük dℓ parçasını alacak olursak bu uzunluk da halkaya teğet olacaktır. dℓ  vektörünün (kırmızı oklar) yönünü de B ile aynı yönde olacak şekilde seçersek kapalı integral pozitif çıkacaktır. Halkanın sınırlarını belirlediği alandan (sarı bölge) I akımı geçmektedir. Bu durumda ;

∮B ⋅dℓ =μoIiç   

denklemi elde edilir.

Sağ vida kuralına göre ise; vidanın ilerleme yönü akım yönünü, vidanın dönüş yönü ise manyetik alanın yönünü gösterir.